Probability Current in Quantum Mechanics
In nonrelativistic 1D quantum mechanics, consider the probability of finding a particle in the interval \([x_1, x_2]\): \[ P_{x_1,x_2} = \int_{x_1}^{x_2} |\Psi(x,t)|^2\, \text{d}x. \] It is interesting to look at how this probability changes in time. Taking a time derivative, and using the Schrodinger equation \[ i \hbar \partial_t \Psi = \frac{-\hbar^2}{2m} \partial_x^2 \Psi + V \Psi \] to simplify things, we get (assuming a real potential) \[ \frac{d P_{x_1, x_2}}{dt} = \frac{\hbar}{2mi}\int_{x_1}^{x_2} \left[ (\partial_x^2 \Psi^*) \Psi - (\partial_x^2 \Psi) \Psi^* \right] \, \text{d}x \] where since \[ \left[ (\partial_x^2 \Psi^*) \Psi - (\partial_x^2 \Psi) \Psi^* \right] = \partial_x \left[ (\partial_x \Psi^*) \Psi - (\partial_x \Psi) \Psi^*\right], \] we can write this as \[ \frac{d P_{x_1, x_2}}{dt} = J(x_1, t) - J(x_2, t), \] where \[ J(x,t) = \frac{\hbar}{2mi} (\Psi^* \partial_x \Psi - \Psi \partial_x \Psi^*) \] is called the “probability current.”
Continuity Equation
The reason for the name is as follows. At the level of the integrand, we have \[ \partial_t |\Psi|^2 = - \partial_x J, \] which in 3 dimensions becomes \[ \partial_t |\Psi|^2 + \nabla \cdot \mathbf{J} = 0. \] We can write this in a more suggestive form by denoting the probability density as \(\rho = |\Psi|^2\), then we have the equation \[ \partial_t \rho + \nabla \cdot \mathbf{J} = 0, \] which is called the continuity equation.
Electromagnetism and Fluid Dynamics
Classical electrodynamics has a continuity equation that has exactly the same form. In electromagnetism, \(\rho\) is the electrical charge density, and \(\mathbf{J}\) is the electrical current density. The continuity equation expresses mathematically the fact that electrical charge is locally conserved.
There is also a similar equation in fluid dynamics. Specifically, for an Eulerian inviscid fluid, local conservation of the fluid is expressed by \[ \partial_t \rho_m + \nabla \cdot (\rho_m \mathbf{v}) = 0, \] where \(\rho_m\) is the mass density of the fluid, and \(\mathbf{v}\) is the fluid velocity. (Inviscid means zero viscosity, and Eulerian means watching a fixed point in space as the fluid flows past.)
Interpretation in Quantum Mechanics
Since quantum mechanics has a continuity equation for the probability density, it is often said that the probability “flows like a fluid.” However, this analogy takes a bit more work to justify. The fact that a continuity equation exists for some scalar quantity does not necessarily mean that quantity behaves like a fluid. In electromagnetism, we do not say that electrical charge “flows like a fluid.” The dynamics of electric charge is governed by Maxwell’s equations, which are not the same as Euler’s equations for fluid flow.
The existence of a continuity equation just means that the quantity in question is locally conserved. In quantum mechanics, probability is locally conserved. Otherwise the theory would not make much sense.
It is possible to make the analogy between the time evolution of probability in quantum mechanics and fluid flow more precise. I will address this in a future blog post. There is an intuition behind the analogy. Take a particle in an infinite square well where the potential is zero on the interval \([0,a]\), and use units where \(\hbar = 2 m = a = 1\). Then the energy eigenfunctions are \[ \psi_n(x) = \sqrt{2} \sin(n\pi x). \] If we start the particle in the superposition state \[ \Psi(x,0) = \sqrt{\frac{2}{3}} \psi_1(x) + \sqrt{\frac{1}{3}} \psi_2(x) \] and time-evolve, the probability density \(|\Psi(x,t)|^2\) behaves like this:
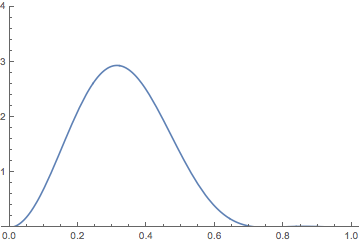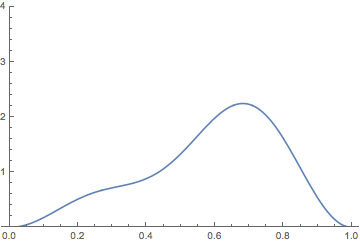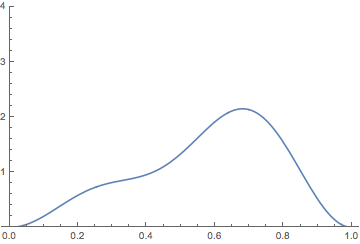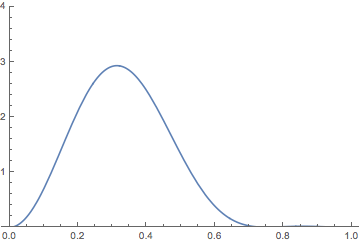
This does evoke fluid-like language such as the probability “sloshing back and forth.”