Introduction
Many mathematicians have a rough mental list of “desert island” books - a small set of books they would choose if stranded on a desert island, forced to spend the winter in a log cabin, or some similiar scenario. Some have published lists of selected books; for example John Baez’s “How to Learn Math and Physics”, “The Mathematics Autodidact’s Aid” by Kristine Fowler, and the “Chicago undergraduate mathematics bibliography” by Christopher Jeris and other contributers. At least one math book is actually set on a desert island: Knuth’s Surreal Numbers.
The MAA (Mathematical Association of America) regularly publishes reviews of mathematical books. They also release the Basic Library List (BLL): a list of books “recommended by the Association for purchase by college and university libraries.” The BLL rates books on the following scale:
| rating | definition |
|---|---|
| BLL | The Basic Library List Committee suggests that undergraduate mathematics libraries consider this book for acquisition. |
| BLL* | The Basic Library List Committee recommends this book for acquisition by undergraduate mathematics libraries. |
| BLL** | The Basic Library List Committee strongly recommends this book for acquisition by undergraduate mathematics libraries. |
| BLL*** | The Basic Library List Committee considers this book essential for undergraduate mathematics libraries. |
In short, no star means “suggested,” 1 star means “recommended,” 2 stars means “strongly recommended,” and 3 stars means “essential.” The list is being actively updated and revised (though I am not sure how often), and a spreadsheet of the latest version can be downloaded here. For the rest of this post I will be using the version of the spreadsheet that was last updated on August 26, 2019.
While the scale of the BLL is certainly above “desert island” or “log cabin” scale, it is interesting to take a broad look at the books and topics that are on the list. The rest of this post consists of a data-driven exploration of the BLL list. I used R to do the analysis (this post is written in R Markdown), but since this post is less tutorial-focused than others, I’m not going to expose the R code.
Data Issues
There are several data issues with the BLL list. Skip this section if you’re not interested - the fun stuff comes later.
First, when reading in the file, I found that that the edition for one book was accidently coded as ‘2nd’ instead of ‘2’:
| title | author | edition | publication_year |
|---|---|---|---|
| Golden Years of Moscow Mathematics | Smilka Zdravkovska and Peter L. Duren, editors | 2nd | 2007 |
Fixing this problem and counting the number of books by edition gives:
| edition | n |
|---|---|
| 1 | 4 |
| 2 | 375 |
| 3 | 137 |
| 4 | 61 |
| 5 | 40 |
| 6 | 30 |
| 7 | 14 |
| 8 | 11 |
| 9 | 5 |
| 10 | 5 |
| 11 | 3 |
| 12 | 1 |
| 13 | 1 |
| 15 | 2 |
| 18 | 1 |
| 27 | 1 |
| 32 | 1 |
| NA | 2296 |
I’m guessing that “NA” implicitly codes for the first edition. Here are the four books with an explicit label of first edition:
| title | author | publication_year | bll_rating |
|---|---|---|---|
| Hex: The Full Story | Ryan B. Hayward and Bjarne Toft | 2019 | BLL |
| Introduction to Probability with Texas H o l d ’em Examples | Frederic Paik Schoenberg | 2012 | BLL |
| Math Art: Truth, Beauty, and Equations | Stephen Ornes | 2019 | BLL |
| The Undecidable: Basic Papers on Undecidable Propositions, Unsolvable Problems and Computable Functions | Martin Davis | 2004 | BLL** |
There are no obvious problems here (besides the odd spaces in the title of Schoenberg’s book). The books with really high edition numbers also deserve a sanity check. Here are all the books listed with edition greater than 10:
| title | author | publication_year | edition |
|---|---|---|---|
| Readings in the History of Mathematics Education | James K. Bidell and Robert G. Clason | 1970 | 32 |
| Machinery’s Handbook 27, Toolbox Edition | Erik Oberg et al. | 2004 | 27 |
| Family Math | Jean Kerr Stenmark, Virginia Thompson, and Ruth Cossey | 1986 | 18 |
| Contemporary Business Mathematics for Colleges | James E. Deitz and James L. Southam | 2008 | 15 |
| Mathematical Crystallography | M. Boisen and G. V. Gibbs | 1990 | 15 |
| Mathematical Recreations and Essays | W.W. Rouse Ball and H.S.M. Coxeter | 1987 | 13 |
| Introductory Mathematical Analysis for Business, Economics and the Life and Social Sciences | Ernest F. Haeussler, Richard S. Paul, and R.J. J. Wood | 2007 | 12 |
| Calculus for Business, Economics, Life Sciences & Social Sciences | Raymond A. Barnett, Michael R. Ziegler, and Karl E. Byleen | 2007 | 11 |
| College Mathematics for Business, Economics, Life Sciences & Social Sciences | Raymond A. Barnett, Michael R. Ziegler, and, Karl E. Byleen | 2007 | 11 |
| Finite Mathematics for Business, Economics, Life Sciences and Social Sciences | Raymond A. Barnett, Michael R. Ziegler, and Karl E. Byleen | 2007 | 11 |
The first book, Readings in the History of Mathematics Education, was published in conjunction with the 32nd Yearbook of the National Council of Teachers of Mathematics, so it is not actually in its 32nd edition. The second entry looks correct, and the book is already up to its 30th edition. Mathematical Crystallography was book 15 in the series “Reviews in Mineralogy.” I didn’t bother checking more or correcting the mistakes, since I’m not going to use the “edition” variable in what follows.
One book is mistakenly listed with a publication year of 2986:
| title | author | edition | publication_year |
|---|---|---|---|
| Probability Distributions | V. Rothschild and N. Logothetis | NA | 2986 |
A quick google search brings up an Amazon listing with a publication date of 1986, which is seconded by a citation in another book. I changed this value to the correct one in what follows.
There also appear to be several duplicate entries in the list. Looking for books with the same title and author gives:
| title | author | count |
|---|---|---|
| A Walk Through Combinatorics: An Introduction to Enumeration and Graph Theory | Miklós Bóna | 3 |
| A Primer on Scientific Programming with Python | Hans Petter Langtangen | 2 |
| A Survey of Modern Algebra | Garrett Birkhoff and Saunders Mac Lane | 2 |
| Additive Combinatorics | Terence Tao and Van H. Vu | 2 |
| Advanced Engineering Mathematics | Erwin Kreyszig | 2 |
| Advanced Modern Algebra | Joseph J. Rotman | 2 |
| Algebraic Number Theory | Richard A. Mollin | 2 |
| An Introduction to Manifolds | Loring W. Tu | 2 |
| An Introduction to Mathematical Cryptography | Jeffrey Hoffstein, Jill Pipher, and Joseph H. Silverman | 2 |
| An Introduction to Tensors and Group Theory for Physicists | Nadir Jeevanjee | 2 |
| An Invitation to Morse Theory | Liviu Nicolaescu | 2 |
| Category Theory | Steve Awodey | 2 |
| Combinatorics of Permutations | Miklós Bóna | 2 |
| Elementary Analysis: The Theory of Calculus | Kenneth A. Ross | 2 |
| Elementary Linear Algebra: Applications Version | Howard Anton and Chris Rorres | 2 |
| Elements of Algebra and Algebraic Computing | John D. Lipson | 2 |
| Episodes in the Mathematics of Medieval Islam | J. L. Berggren | 2 |
| Finite-Dimensional Vector Spaces | Paul R. Halmos | 2 |
| Galois Theory | Steven H. Weintraub | 2 |
| Geometry: Our Cultural Heritage | Audun Holme | 2 |
| Graph Theory | Reinhard Diestel | 2 |
| Handbook of Parametric and Nonparametric Statistical Procedures | David J. Sheskin | 2 |
| Introduction to Analytic and Probabilistic Number Theory | Gérald Tenenbaum | 2 |
| Introduction to Commutative Algebra | M. F. Atiyah and I. G. MacDonald | 2 |
| Introductory Combinatorics | Richard A. Brualdi | 2 |
| Math Through the Ages: A Gentle History for Teachers and Others | William P. Berlinghoff and Fernando Q. Gouvêa | 2 |
| Mathematics and Its History | John Stillwell | 2 |
| Modern Algebra: An Introduction | John R. Durbin | 2 |
| Partial Differential Equations: Analytical and Numerical Methods | Mark S. Gockenbach | 2 |
| Potential Theory | Lester L. Helms | 2 |
| Proofs and Refutations: The Logic of Mathematical Discovery | Imre Lakatos | 2 |
| Proofs from THE BOOK | Martin Aigner and Günter M. Ziegler | 2 |
| Ramsey Theory on the Integers | Bruce M. Landman and Aaron Robertson | 2 |
| The Fourth Dimension and Non-Euclidean Geometry in Modern Art | Linda Dalrymple Henderson | 2 |
| The Principia : Mathematical Principles of Natural Philosophy | Isaac Newton, translated by I. Bernard Cohen and Anne Whitman | 2 |
| The Theory of Island Biogeography | Robert H. MacArthur and Edward O. Wilson | 2 |
| The Variational Principles of Mechanics | Cornelius Lanczos | 2 |
| Thinking Mathematically | J. Mason, L. Burton, and K. Stacey | 2 |
| Using R for Introductory Statistics | John Verzani | 2 |
Taking a closer look at some of these cases reveals that they are different editions of the same book. It is debatable whether multiple editions should be included or not. In general, I think only the latest edition should be included, with the exception being long-used classic works where material gets removed in later editions.
One example of this in physics is Goldstein’s Classical Mechanics - the older second edition contains useful annotated “Suggested References” at the end of each chapter that were removed in the third edition. (The third edition, but not the second, is included in the BLL list, with an “essential” rating.)
I’ll leave the multiple editions alone, and look for cases where author, title, and edition all match:
| title | author | edition | publication_year | publisher | bll_rating | topics | count |
|---|---|---|---|---|---|---|---|
| A Survey of Modern Algebra | Garrett Birkhoff and Saunders Mac Lane | 4 | 1997 | A K Peters | BLL*** | Abstract Algebra | Algebra | Classic Works | 2 |
| A Survey of Modern Algebra | Garrett Birkhoff and Saunders Mac Lane | 4 | 2008 | A K Peters | BLL** | Classic Works | Abstract Algebra | 2 |
| Additive Combinatorics | Terence Tao and Van H. Vu | NA | 2006 | Cambridge University Press | BLL | Combinatorics | Number Theory | 2 |
| Additive Combinatorics | Terence Tao and Van H. Vu | NA | 2010 | Cambridge University Press | BLL | Combinatorics | Number Theory | 2 |
| Elements of Algebra and Algebraic Computing | John D. Lipson | NA | 1981 | Addison-Wesley | BLL | Algebra | Applied Algebra | 2 |
| Elements of Algebra and Algebraic Computing | John D. Lipson | NA | 1981 | Addison-Wesley | BLL | Applied Algebra | Algebra | 2 |
| Finite-Dimensional Vector Spaces | Paul R. Halmos | NA | 1974 | Springer Verlag | BLL*** | Classic Works | Linear Algebra | 2 |
| Finite-Dimensional Vector Spaces | Paul R. Halmos | NA | 2017 | Dover Publications | BLL** | Classic Works | Linear Algebra | 2 |
| Introduction to Commutative Algebra | M. F. Atiyah and I. G. MacDonald | NA | 1994 | Addison Wesley Publishing Company | BLL*** | Commutative Algebra | 2 |
| Introduction to Commutative Algebra | M. F. Atiyah and I. G. MacDonald | NA | 2015 | Westview Press | BLL** | Classic Works | Commutative Algebra | 2 |
| Math Through the Ages: A Gentle History for Teachers and Others | William P. Berlinghoff and Fernando Q. Gouvêa | 2 | 2014 | Oxton House Publishers | BLL* | History of Mathematics | 2 |
| Math Through the Ages: A Gentle History for Teachers and Others | William P. Berlinghoff and Fernando Q. Gouvêa | 2 | 2015 | MAA Press/Oxton House Publishers | BLL** | History of Mathematics | 2 |
| Proofs and Refutations: The Logic of Mathematical Discovery | Imre Lakatos | NA | 1976 | Cambridge University Press | BLL*** | Classic Works | Philosophy of Mathematics | Polyhedra | 2 |
| Proofs and Refutations: The Logic of Mathematical Discovery | Imre Lakatos | NA | 2016 | Cambridge University Press | BLL*** | Philosophy of Mathematics | 2 |
| The Fourth Dimension and Non-Euclidean Geometry in Modern Art | Linda Dalrymple Henderson | NA | 1983 | Princeton University Press | BLL* | Non-Euclidean Geometry | Art | 2 |
| The Fourth Dimension and Non-Euclidean Geometry in Modern Art | Linda Dalrymple Henderson | NA | 2013 | MIT Press | BLL* | History of Mathematics | Mathematics and Culture | Non-Euclidean Geometry | 2 |
| The Principia : Mathematical Principles of Natural Philosophy | Isaac Newton, translated by I. Bernard Cohen and Anne Whitman | NA | 1999 | University of California Press | BLL* | Classic Works | Classical Mechanics | Mathematical Physics | 2 |
| The Principia : Mathematical Principles of Natural Philosophy | Isaac Newton, translated by I. Bernard Cohen and Anne Whitman | NA | 1999 | University of California Press | BLL* | Classic Works | History of Mathematics | Mathematical Physics | 2 |
| The Theory of Island Biogeography | Robert H. MacArthur and Edward O. Wilson | NA | 2001 | Princeton University Press | BLL | Mathematical Biology | Mathematical Modeling | 2 |
| The Theory of Island Biogeography | Robert H. MacArthur and Edward O. Wilson | NA | 2001 | Princeton University Press | BLL | Mathematical Biology | 2 |
There are 10 books here, and the double listings seem to be genuine errors. Perhaps the committee behind BLL should take a closer look (I plan to send them an email when I publish this blog post). Some books seem to be repeated with slightly different topic listings, some with slightly different names for the publisher, and I am not sure why the 1997 printing of A Survey of Modern Algebra gets an “essential” rating while the 2008 printing only gets “strongly recommended.”
Since there are only 10 books out of close to 3000 total that are “double listed,” I decided to just leave them alone for the following analysis.
Finally, there are several data errors in the “publisher” variable. Counting the most common publishers:
| publisher | books | percent_of_total |
|---|---|---|
| Springer | 319 | 10.7 |
| Dover Publications | 300 | 10.0 |
| Springer Verlag | 210 | 7.0 |
| John Wiley | 180 | 6.0 |
| Cambridge University Press | 178 | 6.0 |
| American Mathematical Society | 144 | 4.8 |
| Mathematical Association of America | 141 | 4.7 |
| Princeton University Press | 134 | 4.5 |
| Oxford University Press | 101 | 3.4 |
| Birkhäuser | 80 | 2.7 |
Springer and Springer Verlag together make up about 18% of the list, which is not surprising for math books. I was a bit surprised by Dover taking second place.
Scrolling through the entire list of publishers reveals several data issues, such as “princeton University Press,” “Princeton Universy Press” and other misspellings and typos. One publisher shows up as “hapman & Hall/CRC,” “Chapman/CRC,” “Chapman Hall/CRC,” “Chapman and Hall/CRC,” “Chapman & Hill/CRC,” “Chapman & Hall,” “CRC/Chapman & Hall,” “CRC Press,” “Chapman&Hall/CRC,” and “Chapman & Hall/CRC.” The final variant is the most common (78 books, or 2.6% of the total), and adding together all of the variants does change the list of the top 10 publishers:| publisher | n | percent |
|---|---|---|
| Springer | 319 | 10.7 |
| Dover Publications | 300 | 10.0 |
| Springer Verlag | 210 | 7.0 |
| John Wiley | 180 | 6.0 |
| Cambridge University Press | 178 | 6.0 |
| American Mathematical Society | 144 | 4.8 |
| Mathematical Association of America | 141 | 4.7 |
| Princeton University Press | 134 | 4.5 |
| Oxford University Press | 101 | 3.4 |
| Chapman & Hall/CRC | 93 | 3.1 |
As with the “edition” variable, I did not extensively dig into the “publisher” variable or bother fixing the mistakes, since I’m not going to use it. The variables that I am most interested in and that I will explore in the following sections are author, publication date, topics, and ratings.
Publication Date
When were the books on the BLL list published? Here is a plot of the number of books published by year:
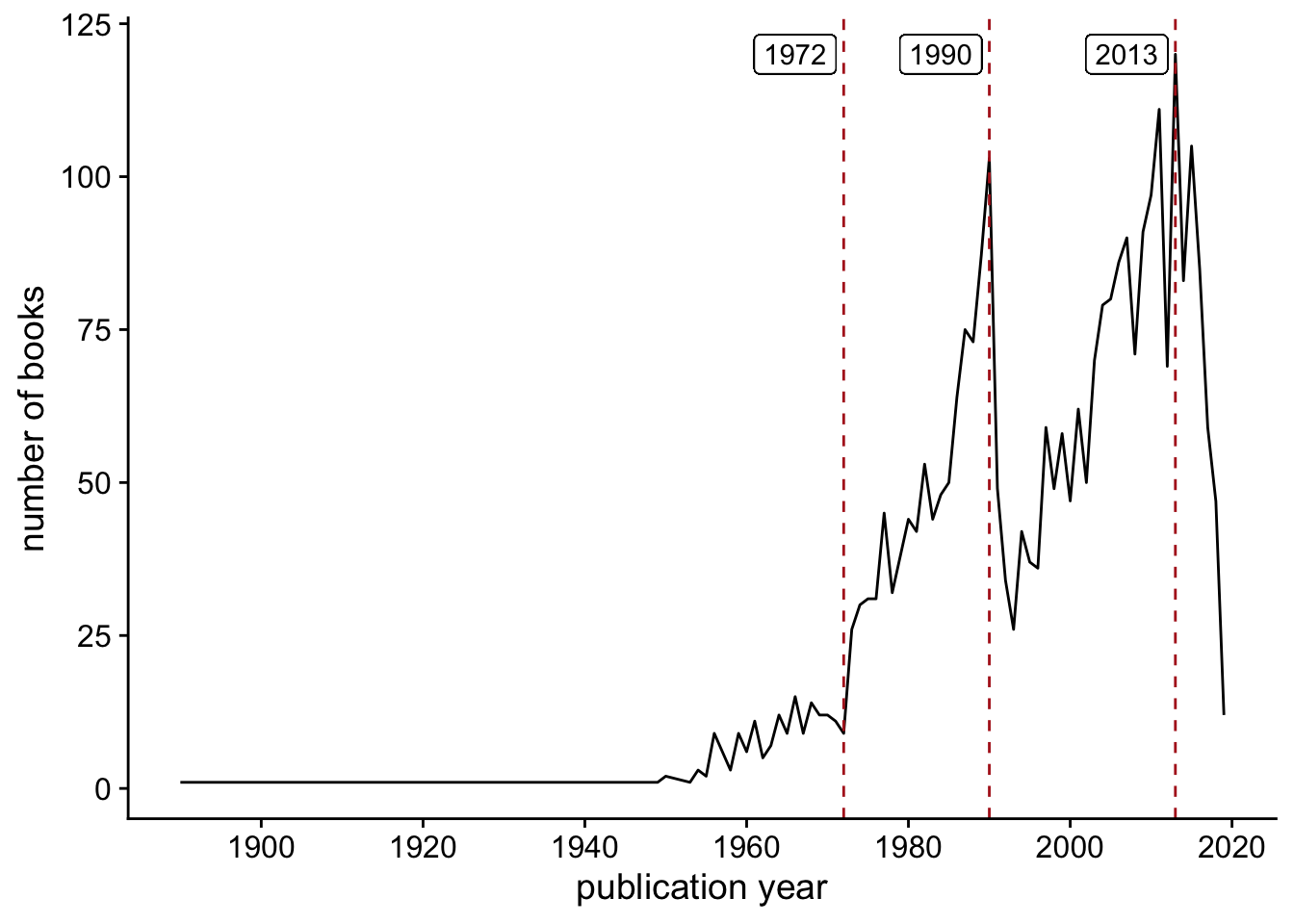
This is a very interesting time series. First, here are the 10 earliest books:
| title | author | publication_year |
|---|---|---|
| The Teaching and History of Mathematics in the United States | Florian Cajori | 1890 |
| Projective Geometry | Oswald Veblen and John Wesley Young | 1910 |
| Treatise on the Mathematical Theory of Elasticity | Augustus E. Love | 1927 |
| Leçons sur la Théorie Mathématique de la Lutte pour la Vie | Vito Volterra | 1931 |
| Greek Mathematical Works, Volume I: Thales to Euclid | Ivor Thomas, translator | 1939 |
| Rings and Ideals | Neal H. McCoy | 1948 |
| Divergent Series | G. H. Hardy | 1949 |
| Elgenfunction Expansions Associated With Second Order Differential Equations | E. C. Titchmarsh | 1950 |
| Nonlinear Vibrations In Mechanical and Electrical Systems | J J Stoker | 1950 |
| Abstract Set Theory | Abraham Fraenkel | 1953 |
The book by Volterra is in French; Google translate gives “Lessons on the Mathematical Theory of the Struggle for Life.” I don’t think that many American undergraduate math majors can read French. Out of curiousity, I checked and the list does contain Whittaker and Watson’s A Course of Modern Analysis, but a 4th edition published in 1996 (the first edition was published in 1902).
After a brief dip in 1972 (9 books), things pick up in 1973 (26 books), and stay fairly consistently high until reaching a peak in 1990 (103 books). There is then a collapse that bottoms out in 1993 (26 books), and then things pick up again and reach a global maximum in 2013 with 120 books. Maybe someone with a closer connection to mathematical publishing can explain this. What was so special about 1990 and the preceding years, and why do things decline so quickly right after that?
The list includes 12 books with a publication year of 2019, and I assume that the number will grow as the list is updated.
Topics
Each book has one or several associated topics. Here are the top 20 by the number of books tagged with that topic. The topics are not exclusive, so the percentages can add up to more than 100. For example, a book could be tagged with both “Classic Works” and “Algebra.”
| topics | n | percent |
|---|---|---|
| History of Mathematics | 424 | 14.2 |
| Mathematics for the General Reader | 192 | 6.4 |
| Statistics | 151 | 5.1 |
| Mathematical Biology | 126 | 4.2 |
| Mathematics Education | 122 | 4.1 |
| Biography | 112 | 3.7 |
| Combinatorics | 111 | 3.7 |
| Classic Works | 110 | 3.7 |
| Number Theory | 104 | 3.5 |
| Geometry | 93 | 3.1 |
| Real Analysis | 87 | 2.9 |
| Algebra | 84 | 2.8 |
| Mathematical Modeling | 84 | 2.8 |
| Analysis | 79 | 2.6 |
| Mathematical Physics | 78 | 2.6 |
| Partial Differential Equations | 72 | 2.4 |
| Logic | 70 | 2.3 |
| Calculus | 69 | 2.3 |
| Linear Algebra | 69 | 2.3 |
| Abstract Algebra | 66 | 2.2 |
| Surveys of Mathematics | 65 | 2.2 |
The vastly predominant category is “History of Mathematics.” I was surprised that “Mathematics for the General Reader,”, “Mathematical Biology,” “Mathematics Education,” and “Biography” are all more numerous than “classic” categories like “Real Analysis,” “Number Theory,” and “Algebra.”
I thought that perhaps “History of Mathematics” might be so dominant because each subfield has its own history, so there would be history of number theory, history of algebra, etc., each tagged with the subfield as well as “History of Mathematics.” To check this, I looked at the categories most often combined with “History of Mathematics.” Here are the top 10:
| topics | n |
|---|---|
| History of Mathematics | 93 |
| Biography | History of Mathematics | 50 |
| Classic Works | History of Mathematics | 26 |
| History of Mathematics | Non-Western Cultures | 14 |
| History of Mathematics | Mathematics Education | 9 |
| Biography | History of Mathematics | Women in Mathematics | 8 |
| Calculus | History of Mathematics | 8 |
| History of Mathematics | Mathematics for the General Reader | 8 |
| History of Mathematics | Philosophy of Mathematics | 7 |
| History of Mathematics | Biography | 6 |
It looks like my hypothesis is wrong - the only grouping of the type I was thinking of is “Calculus | History of Mathematics.” These 10 category groupings contain 229 books, so “History of Mathematics” would still be on top only including these 10. I am not sure what I think about this. History is important, to be sure, but should the ideal math library lean so heavily towards history, especially an undergraduate library? Often tracing the historical development of a subject is not the best way to learn that subject. A good example from physics is quantum mechanics. Learning quantum mechanics for the first time by reading through the history doesn’t really work - the fundamental principles tend to get obscured by unneccessary historical detail. On the other hand, history can catch the interest of students and provide glimpses of mathematical “culture.”
On a similar note, here are the most common topic groupings containing “Classic Works:”
| topics | n |
|---|---|
| Classic Works | History of Mathematics | 26 |
| Analytic Number Theory | Classic Works | History of Mathematics | Number Theory | 3 |
| Classic Works | Classical Algebra | History of Mathematics | 3 |
| Classic Works | Geometry | History of Mathematics | 3 |
| Classic Works | Recreational Mathematics | 3 |
| Abstract Algebra | Classic Works | 2 |
| Classic Works | History of Mathematics | Mathematical Physics | 2 |
| Classic Works | History of Mathematics | Non-Euclidean Geometry | 2 |
| Classic Works | History of Mathematics | Non-Western Cultures | 2 |
| Classic Works | Linear Algebra | 2 |
What were the topics of books published in that prolific year of 1990? Here are the top 5:
| topics | n |
|---|---|
| Mathematics Education | 20 |
| History of Mathematics | 19 |
| Teaching Mathematics | 9 |
| Biography | 6 |
| Statistics | 6 |
Ratings
Now we come to the most exciting part of the BLL list - the ratings! First, a breakdown of the number of books given each rating:| bll_rating | n | percent |
|---|---|---|
| BLL | 1419 | 47.5 |
| BLL* | 931 | 31.2 |
| BLL** | 451 | 15.1 |
| BLL*** | 187 | 6.3 |
So about 1 in 16 books get the coveted “essential” rating (BLL***). At an average price of $50 per book, you could purchase the “essential” library for under $10,000. (I don’t actually know if the average price would come out to $50 per book. It might be higher.)
How does the rating relate to the publication year? (In this plot and the following one, I only included years in which more than 1 book was published.)
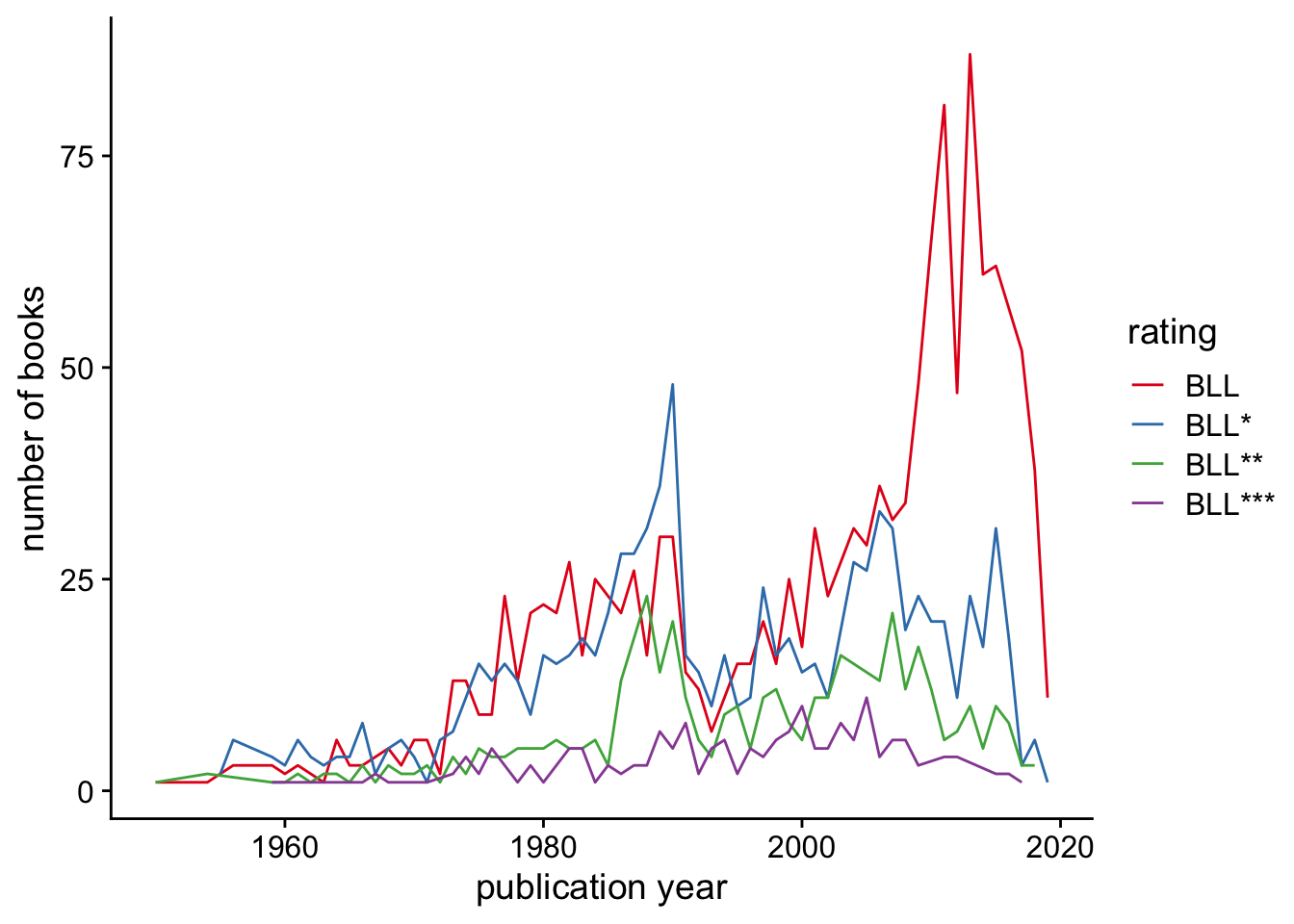
Another way to look at this is to plot the percentage of books published each year that received a given rating:
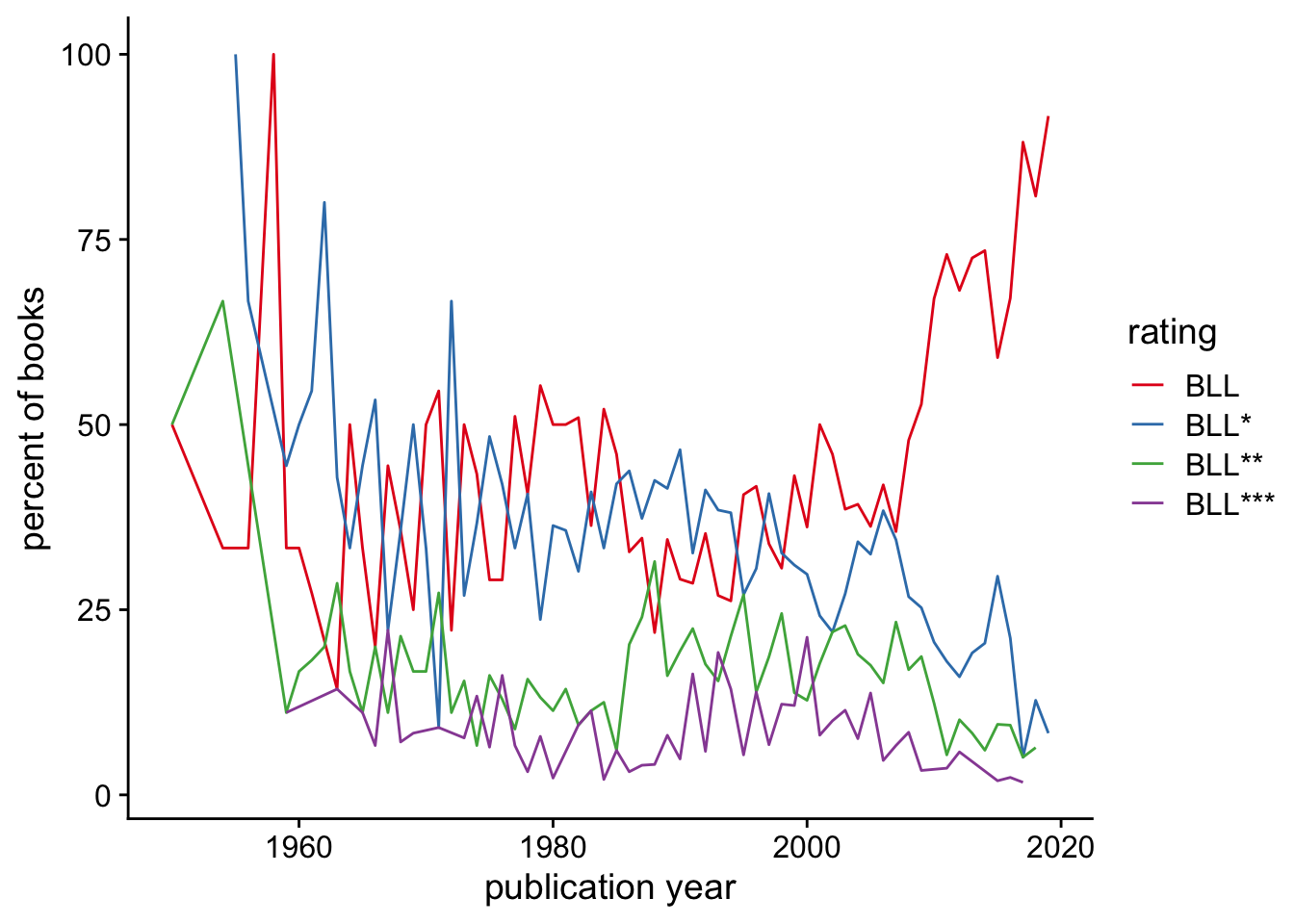
The proportion of books that are just “suggested” has increased rapidly in recent years: from 36% in 2007 to 92% in 2019. This could be because more low-quality books are getting published, or it could be because it takes longer to evaluate the quality of “essential” books - some of the 2019 “suggested” books might have their ratings upgraded to “essential” as time goes on.
What is the makeup by topic of the “essential” undergraduate math library? There are 122 distinct topics for the 186 books. In the entire list (all ratings included), there are 354 distinct topics. Here are the 20 most common topics that are not included in the essential library:
| topic | books |
|---|---|
| Differential Geometry | 54 |
| Functional Analysis | 37 |
| Algebraic Geometry | 33 |
| Transition to Advanced Mathematics | 31 |
| Representation Theory | 25 |
| Technical Mathematics | 21 |
| Measure Theory | 19 |
| Proofs and Logic | 19 |
| Cryptography | 18 |
| Low-dimensional Topology | 18 |
| Finance | 17 |
| Actuarial Science | 15 |
| Applied Algebra | 15 |
| Lie Groups | 15 |
| Engineering Mathematics | 14 |
| Operator Theory | 14 |
| Category Theory | 13 |
| Visualization | 13 |
| Inequalities | 11 |
| Liberal Arts Mathematics | 11 |
| Mathematical Software | 11 |
| Model Theory | 11 |
| Multivariate Statistics | 11 |
| Transformation Geometry | 11 |
Many of these topics are specialized and lean more towards graduate-level than undergraduate level. One that I find surprising is Inequalities - in my opinion a book like The Cauchy-Schwarz Master Class by Steele deserves an “essential” rating rather than just the “strongly recommended” rating it was given.
Here are the 20 most common topics that are included in the essential library:
| topic | books |
|---|---|
| History of Mathematics | 19 |
| Mathematics for the General Reader | 17 |
| Classic Works | 12 |
| Statistics | 11 |
| Surveys of Mathematics | 10 |
| Mathematical Modeling | 8 |
| Mathematical Physics | 8 |
| Teaching Mathematics | 8 |
| Algorithms | 7 |
| Mathematical Biology | 7 |
| Recreational Mathematics | 7 |
| Abstract Algebra | 6 |
| Combinatorics | 6 |
| Mathematics Education | 6 |
| Non-Western Cultures | 6 |
| Number Theory | 6 |
| Algebra | 5 |
| Analytic Number Theory | 5 |
| Biography | 5 |
| Geometry | 5 |
I looked specifically for some books and was surprised by their omission - for example Gradshteyn and Ryzhik was only included at the base “BLL” level. From the physics point of view, I was surprised that Goldstein’s Classical Mechanics was included in the top-rated books, while the Feynman Lectures on Physics were not included at all. Goldstein’s book is often used as a graduate level text, and the Feynman Lectures certainly seem more appropriate for undergrads.
But these are small quibbles - any list of books inherently invites criticism from individual opinions of its sins of omission and commission. That is part of the value of the list - it invites you to argue with it! Lists are also valuable for their serendipity. While working with the BLL list, I came across several books that I made note of to peruse in the future.