Given two positive numbers \(a\) and \(b\), the most well-known way to average them is to take the sum divided by two. This is often called the average or the mean of \(a\) and \(b\), but to distinguish it from other means it is called the arithmetic mean: \[ \text{arithmetic mean} = \frac{a + b}{2}. \]
Another common, and useful, type of mean is the geometric mean. For two positive numbers \(a\) and \(b\), \[ \text{geometric mean} = \sqrt{ab}. \]
A famous inequality, the AM-GM inequality (AM for arithmetic mean, GM for geometric mean) states that the geometric mean is always smaller than or equal to the arithmetic mean: \[ \sqrt{ab} \leq \frac{a + b}{2}. \] The two sides are only equal if \(a = b\).
These two means can of course be extended to more than two positive numbers. For \(n\) positive numbers \(\{ x_1, x_2, \dots \, x_n\}\), the arithmetic mean becomes \[ \frac{1}{n} \sum_{i=1}^n x_i, \] and the geometric mean becomes \[ \sqrt[n]{x_1 x_2 \cdots x_n}, \] so the AM-GM inequality is \[ \sqrt[n]{x_1 x_2 \cdots x_n} \leq \frac{1}{n} \sum_{i=1}^n x_i. \]
Why is the geometric mean useful? There are different reasons it is useful for different applications, but in physics we are often interested in estimating quantities to the nearest power of 10 (an order-of-magnitude estimate). Doing this type of estimate is much faster than doing a detailed calculation, and can tell us whether or not a detailed calculation is even necessary.
If you are doing an order of magnitude estimation, and can guess an upper bound and a lower bound of some quantity to the nearest powers of 10, then taking the geometric mean is a good way to average your bounds. In symbols, say your upper bound is \(10^b\) and your lower bound is \(10^a\) (so \(a < b\)). Then the geometric mean gives \[ \sqrt{10^a 10^b} = (10^a 10^b)^{1/2} = 10^{\frac{1}{2}(a + b)}. \] So the geometric mean has resulted in the arithmetic mean of the exponents! This is useful because it prevents your upper bound from dominating the average. If your lower bound is \(10^2\) and your upper bound is \(10^8\), then the geometric mean gives \(10^5 = 100,000\) while the arithmetic mean gives approximately \(5 \times 10^7\) (\(50,000,050\) exactly).
It is useful to visually compare the two means (using Mathematica). Go back to the case of two positive numbers \(a\) and \(b\), and fix \(b = 2\), allowing \(a\) to vary:
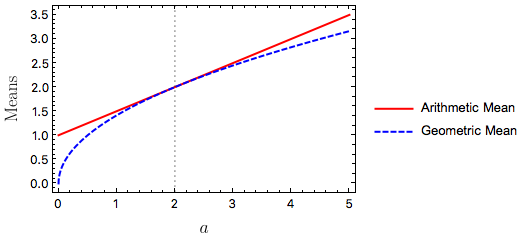
The vertical dotted line is at \(a = 2\) where the two means are equal.
If instead we fix \(b = 1/2\) we get
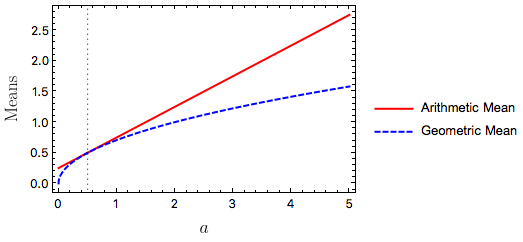
Again, the vertical dotted line is at \(a = 1/2\) where the two means are equal. Here it is especially clear that the geometric mean is less sensitive to the upper bound (\(a\) when \(a > 1/2\)) than the arithmetic mean is.
Interested in finding out how physics, applied math, and data science can help your project or organization? Contact me at landonlehman@gmail.com for a free 15 minute consultation.