It is interesting to look at what happens when you try to “fit” the absolute value function using polynomials. Pick some number \(N\) of points on the absolute value function, and you can find a polynomial of degree \(N - 1\) that goes through those points.
Here is the absolute value function, \(f(x) = |x|\):
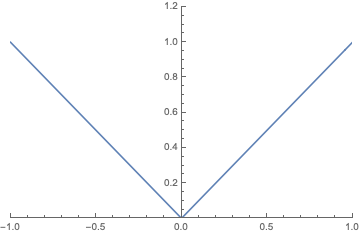
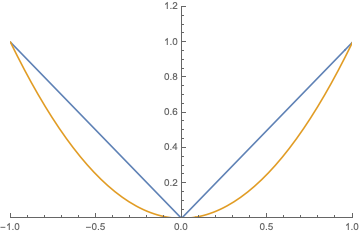
For simplicity, I’ll use an odd number of evenly spaced points so that the resulting polynomial will be even, since \(|x|\) is even. For example, fitting the \((x,y)\) pairs \( (-1, 1)\), \((0, 0)\), and \((1,1)\) with a quadratic polynmial \(a x^2 + b x + c\) results in \(b = c = 0\), and \(a = 1\). You can solve the system of equations to get this fairly easily by hand, but Mathematica has a function that will do the work for you:
Simplify[InterpolatingPolynomial[{{-1, 1}, {0, 0}, {1, 1}}, x]]
returns \(x^2\).
Plotting the interpolating polynomial and \(|x|\) together looks like this:
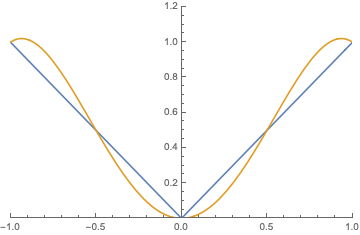
The 4th-order polynomial that fits the 5 evenly-spaced points \((-1, 1)\), \((-1/2, 1/2)\), \((0, 0)\), \((1/2, 1/2)\), and \((1, 1)\) is
\[ -\frac{4}{3} x^4 + \frac{7}{3} x^2 .\]
Here is what the fit looks like:
Not bad, you might say. However, things quickly start to go wrong if we continue this procedure. Let’s automate it first. The interpolation points can be generated using Mathematica’s Table function. For example,
Table[{x, Abs[x]}, {x, -1, 1, 1/3}]
gives these 7 evenly spaced points
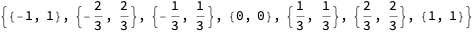
Using this method to generate the 6th, 8th, and 10th order interpolating polynomials:
Expand[InterpolatingPolynomial[Table[{x, Abs[x]}, {x, -1, 1, 1/3}], x]]
Expand[InterpolatingPolynomial[Table[{x, Abs[x]}, {x, -1, 1, 1/4}], x]]
Expand[InterpolatingPolynomial[Table[{x, Abs[x]}, {x, -1, 1, 1/5}], x]]
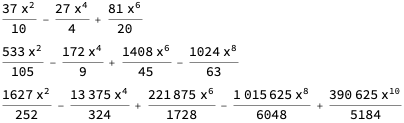
On a plot, along with \(|x|\):
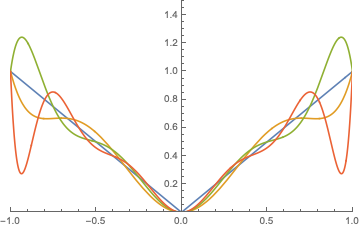
I didn’t label the curves, but you can differentiate them by the fact that the fit gets worse near \(x = -1\) and \(x = 1\) as the order of the polynomial increases. Trying higher and higher orders by using more interpolation points just makes the error worse. Here is the maximum absolute error for \(x \in (-1, 1)\) for polynomials found using this method, where the polynomial order ranges from 2 to 20:
Table[
FindMaximum[
{Abs[Abs[x] - InterpolatingPolynomial[Table[{x, Abs[x]},
{x, -1, 1, 1/y}], x]], 0 < x < 1}, {x, 1}][[1]],
{y, 1, 10, 1}]
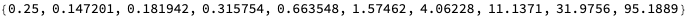
By the time we get to a 20th-order polynomial, the maximum error is almost 100!
This is one reason why polynomial regression is generally not a good idea.