Take a uniform distribution on \([-1, 1]\), so \(p(x) = 1/2\). Pick a single point from this distribution. The probability that this point is within a distance \(m\) from the origin is \(2m/2 = m\). The probability that this point is not within a distance \(m\) from the origin is then \(1-m\).
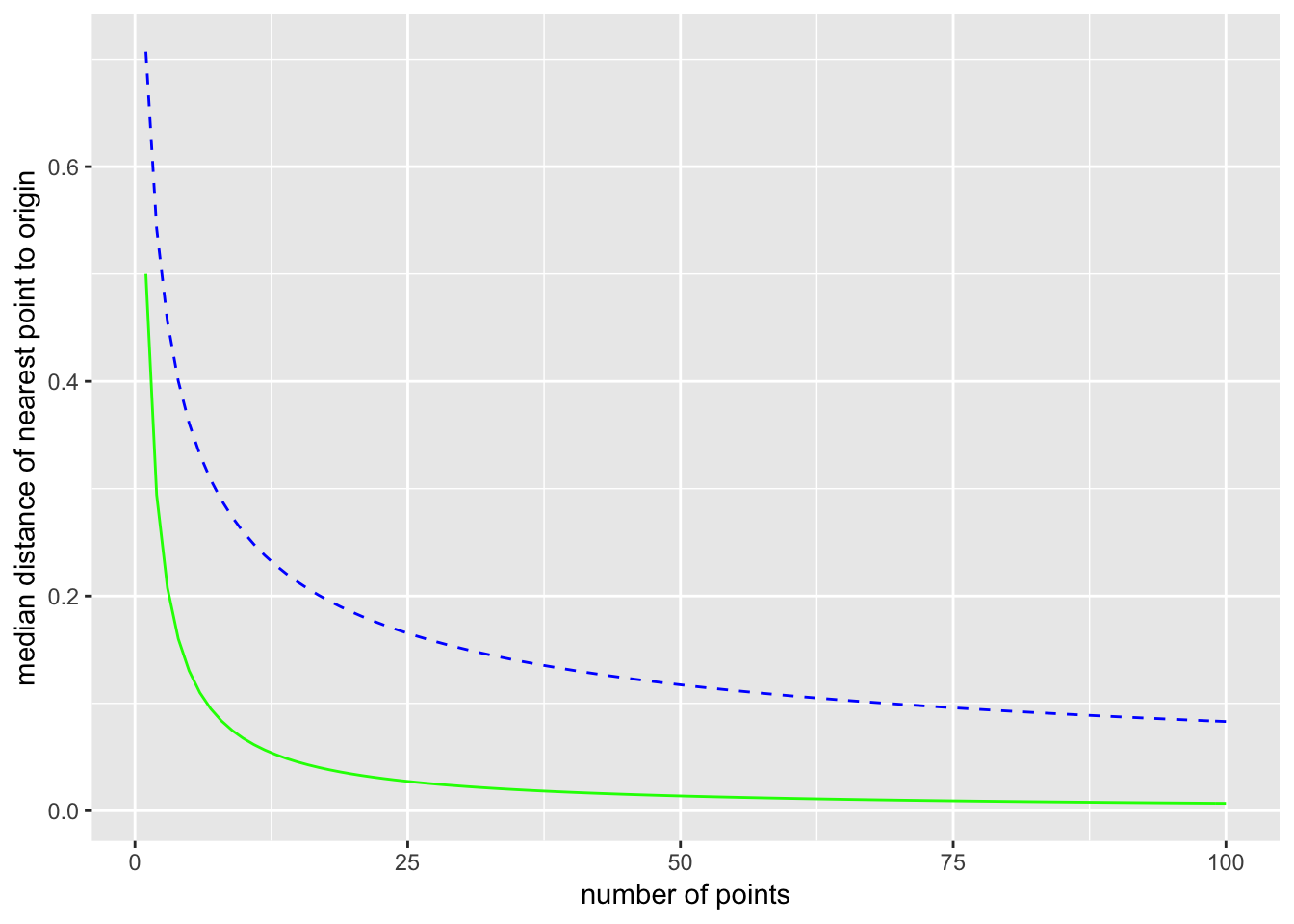
Now consider picking \(N\) points from the distribution. The probability that all \(N\) points are further than \(m\) from the origin is \((1-m)^N\). (Since \(m < 1\), this number gets smaller as \(N\) increases.) Now if we let \(m\) mean the median distance from the origin to the nearest of the \(N\) points, then by the definition of median \[ \text{Pr}(\text{all}\,N\, \text{points are futher than } m \text{ from the origin}) = \frac{1}{2} .\] Setting the two expressions equal \[ (1 - m)^N = \frac{1}{2}, \] and solving for \(m\) gives \[ m = 1 - \left( \frac{1}{2}\right)^{\frac{1}{N}} .\] For \(N = 10\), \(m = 0.07\), and for \(N = 100\), \(m = 0.007\). Of course, as \(N\) goes to infinity, the median distance \(m\) to the nearest point goes to zero.
Now expand this to the 2-dimensional unit ball with a uniform distribution. Here the probability of finding a point in any infinitesimal area element \(\text{d}A = \text{d}x\,\text{d}y\) is the same for all area elements in the unit ball (a circle of radius 1). The area is \(\pi\), so \(p(x,y) = 1/\pi\). The probability of a single point from this uniform distribution being within a distance \(m\) from the origin is the ratio of the area contained within radius \(m\) to the total area: \[ \frac{\pi m^2}{\pi} = m^2. \] The probability of taking \(N\) points and having none of them be within a distance \(m\) of the origin is then \[ (1 - m^2)^N. \] Again let \(m\) be the median distance to the nearest point, so we have the equation \[ (1 - m^2)^N = \frac{1}{2}. \] Solving for \(m\) gives \[ m = \left( 1 - \left(\frac{1}{2}\right)^{\frac{1}{N}} \right)^{\frac{1}{2}}. \] For \(N = 10\), \(m = 0.26\), and for \(N = 100\), \(m = 0.08\). The median distance to the nearest point is larger in 2 dimensions than it is in one dimension. The distance still goes to zero as \(N\) goes to infinity, but it does so more slowly.
Here is a plot comparing one and two dimensions (1D is solid green and 2D is dashed blue):
This can be further generalized to \(p\) dimensions. The volume of a \(p\)-dimensional ball of radius \(R\) is \[ V_p (R) = \frac{\pi^{p/2}}{\Gamma(\frac{p}{2} +1)} R^p, \] and the constants will cancel out when taking ratios. So the probability that a single point chosen from a uniform distribution over the ball is closer than a distance \(m\) from the origin is \(m^p\). Proceeding as we did for one and two dimensions, the median distance of the closest point in \(p\)-dimensions is \[ m = \left(1 - \left(\frac{1}{2}\right)^{\frac{1}{N}}\right)^{\frac{1}{p}}. \] Here is a plot comparing dimensions 1, 2, 10, and 100. (1 is the bottom green line, 2 is the dashed blue line, 10 is the solid red line, and 100 is the dot-dashed black line.)
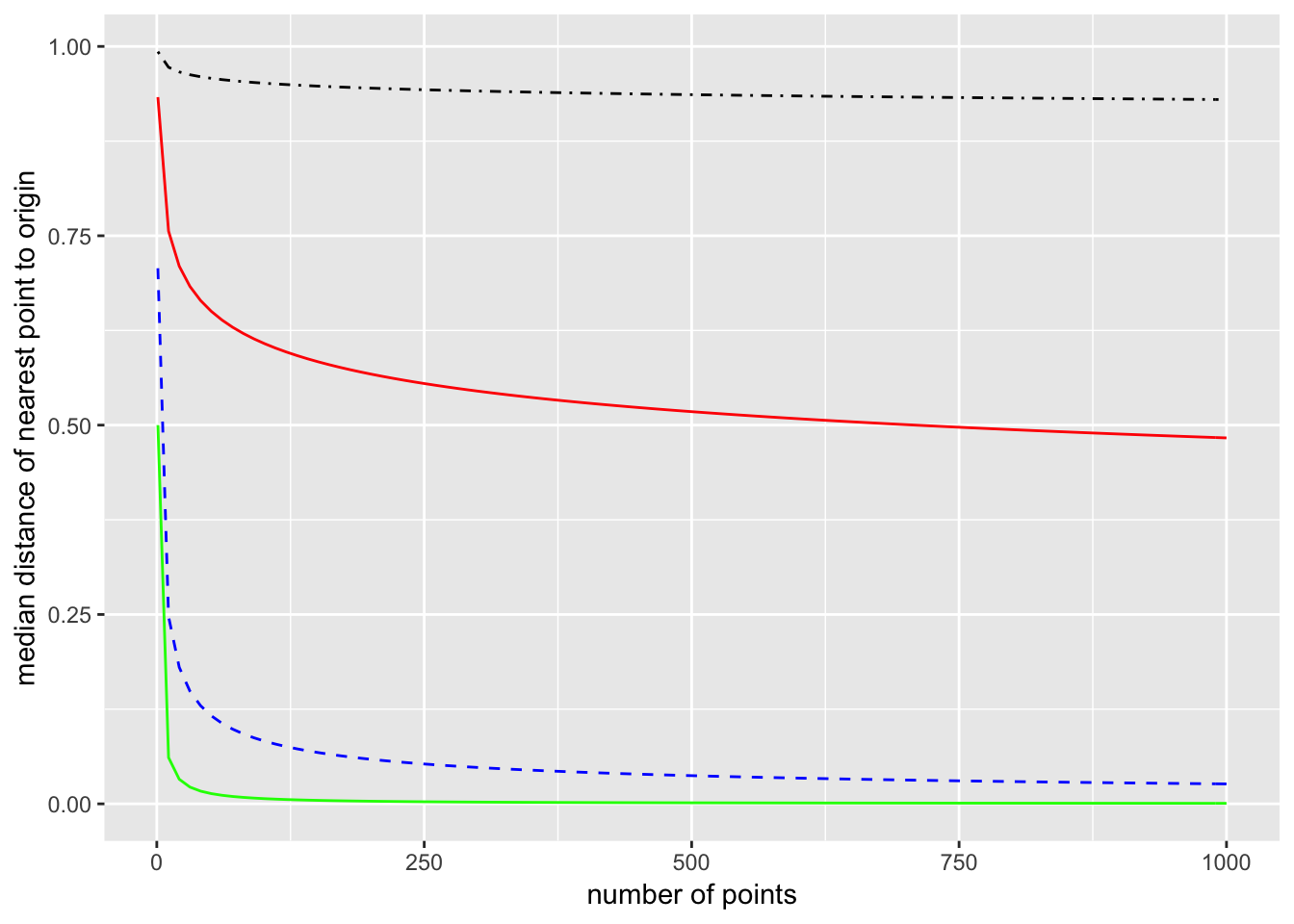
The takeaway is that in high dimensions, you will probably have to go most of the way to the boundary before you encounter a single data point. If the dimension is \(p = 100\), then you have to have samples of around \(10^{12}\) points before the median distance from the origin to the nearest point is \(0.75\).