Take a uniform distribution on $[-1, 1]$, so $p(x) = 1/2$. Pick a single point from this distribution. The probability that this point is within a distance $m$ from the origin is $2m/2 = m$. The probability that this point is not within a distance $m$ from the origin is then $1-m$.
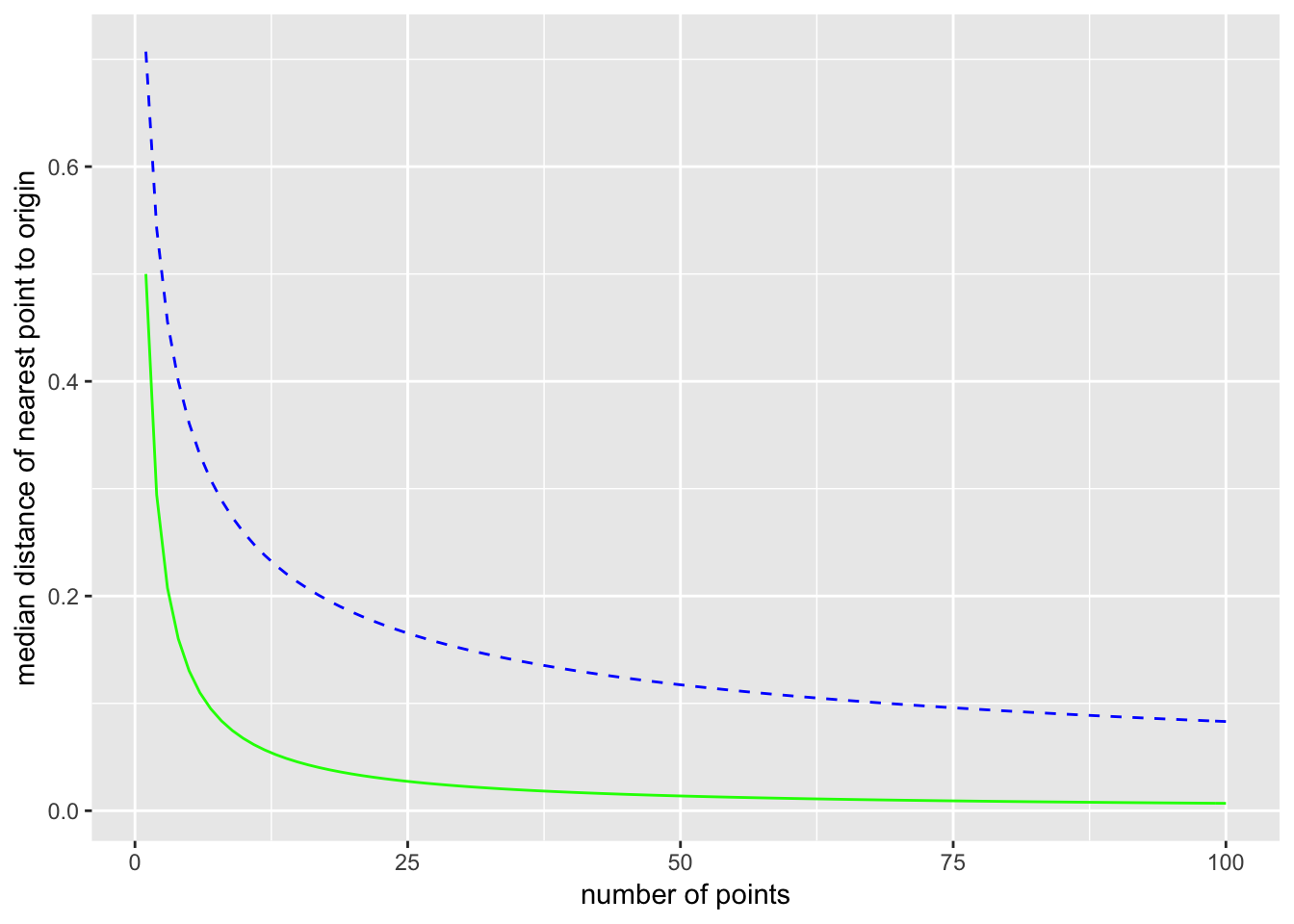
Now consider picking $N$ points from the distribution. The probability that all $N$ points are further than $m$ from the origin is $(1-m)^N$. (Since $m < 1$, this number gets smaller as $N$ increases.) Now if we let $m$ mean the median distance from the origin to the nearest of the $N$ points, then by the definition of median $$ \Pr(\text{all } N \text{ points are further than } m \text{ from the origin}) = \frac{1}{2}. $$ Setting the two expressions equal $$ (1 - m)^N = \frac{1}{2}, $$ and solving for $m$ gives $$ m = 1 - \left( \frac{1}{2}\right)^{\frac{1}{N}}. $$ For $N = 10$, $m = 0.07$, and for $N = 100$, $m = 0.007$. Of course, as $N$ goes to infinity, the median distance $m$ to the nearest point goes to zero.
Now expand this to the 2-dimensional unit ball with a uniform distribution. Here the probability of finding a point in any infinitesimal area element $\mathrm{d}A = \mathrm{d}x,\mathrm{d}y$ is the same for all area elements in the unit ball (a circle of radius 1). The area is $\pi$, so $p(x,y) = 1/\pi$. The probability of a single point from this uniform distribution being within a distance $m$ from the origin is the ratio of the area contained within radius $m$ to the total area: $$ \frac{\pi m^2}{\pi} = m^2. $$ The probability of taking $N$ points and having none of them be within a distance $m$ of the origin is then $$ (1 - m^2)^N. $$ Again let $m$ be the median distance to the nearest point, so we have the equation $$ (1 - m^2)^N = \frac{1}{2}. $$ Solving for $m$ gives $$ m = \left( 1 - \left(\frac{1}{2}\right)^{\frac{1}{N}} \right)^{\frac{1}{2}}. $$ For $N = 10$, $m = 0.26$, and for $N = 100$, $m = 0.08$. The median distance to the nearest point is larger in 2 dimensions than it is in one dimension. The distance still goes to zero as $N$ goes to infinity, but it does so more slowly.
Here is a plot comparing one and two dimensions (1D is solid green and 2D is dashed blue):
This can be further generalized to $p$ dimensions. The volume of a $p$-dimensional ball of radius $R$ is $$ V_p (R) = \frac{\pi^{p/2}}{\Gamma!\left(\frac{p}{2} +1\right)} R^p, $$ and the constants will cancel out when taking ratios. So the probability that a single point chosen from a uniform distribution over the ball is closer than a distance $m$ from the origin is $m^p$. Proceeding as we did for one and two dimensions, the median distance of the closest point in $p$ dimensions is $$ m = \left(1 - \left(\frac{1}{2}\right)^{\frac{1}{N}}\right)^{\frac{1}{p}}. $$ Here is a plot comparing dimensions 1, 2, 10, and 100. (1 is the bottom green line, 2 is the dashed blue line, 10 is the solid red line, and 100 is the dot-dashed black line.)
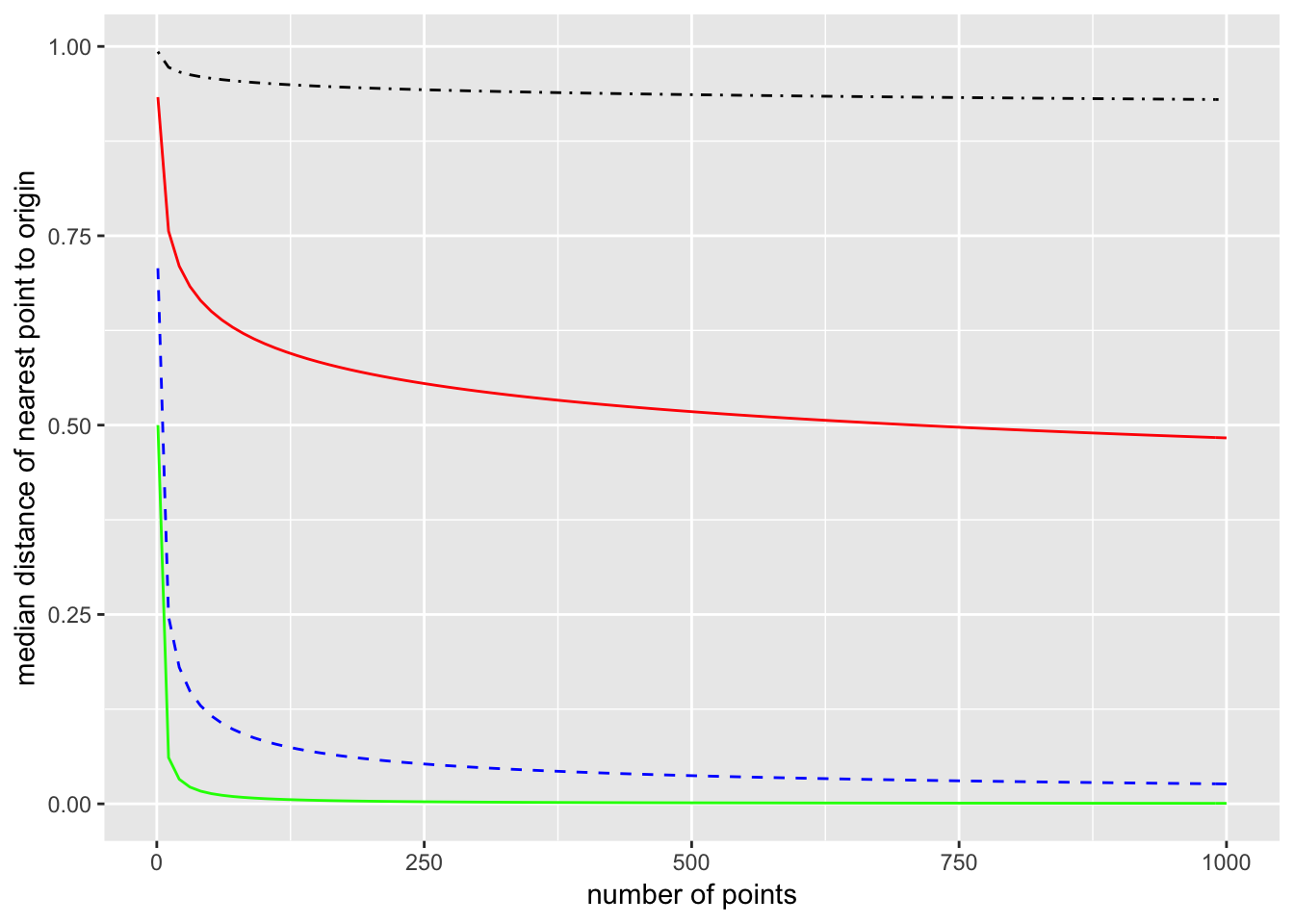
The takeaway is that in high dimensions, you will probably have to go most of the way to the boundary before you encounter a single data point. If the dimension is $p = 100$, then you have to have samples of around $10^{12}$ points before the median distance from the origin to the nearest point is $0.75$.