In my last post, I calculated the mean distance to the nearest point to the origin among \(N\) points taken from a uniform distribution on \([-1, 1]\). This turned out to be \(r = 1/(N+1)\), which is close to but greater than the median distance \(m = 1 - (1/2)^{1/N}\).
In this post, I want to generalize the calculation of the mean to a \(p\)-dimensional uniform distribution over the unit ball. To start things off, let’s look at the specific case \(p = 2\) (a circle). It is often easier to see a generalization after performing the calculation in a few easy (low) dimensional cases.
Following the same form of reasoning as in the previous post, we want to calculate \[ \text{Pr}(\text{ closest point is at } r) = \text{Pr}(\text{ all other points are } > r) \times \text{Pr}(\text{ one point is at } r) .\] The probability that all other points \((N -1)\) are at distances greater than \(r\) is \((1-r^2)^{N-1}\). The probability that one point is at a distance \(r\) is the ratio of the infinitesimal area at \(r\) to the entire area of the unit circle: \[ \frac{2 \pi r\, \text{d}r}{\pi} = 2 r\, \text{d}r. \] We also have to mutiply by an overall factor of \(N\) to account for the \(N\) different ways of labelling the closest point. Putting everything together: \[ \text{Pr}(\text{ closest point is at } r) = 2 r N (1- r^2)^{N-1} \text{d} r, \] and to get the mean value of \(r\) we multiply by \(r\) and integrate: \[ \text{E}(r) = \int_0^1 2 r^2 N (1-r^2)^{N-1} \text{d}r = N \sqrt{\frac{\pi}{4}} \frac{\Gamma(N)}{\Gamma(N + \frac{3}{2})}.\] I used Mathematica to carry out the integral and verified the answer with Gradshteyn and Ryzhik, 3.251, number 1 (page 324 in the 7th edition). In Gradshteyn and Ryzhik, the integral is given in terms of the beta function (Euler integral of the first kind): \[ B(x, y) = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}. \] I don’t see a nice simplified form, and Mathematica doesn’t seem to be able to find one.
Here is a plot made in Mathematica comparing the median distance to the nearest point (\(m = (1 - (1/2)^{1/N})^{1/2}\)) to the mean:
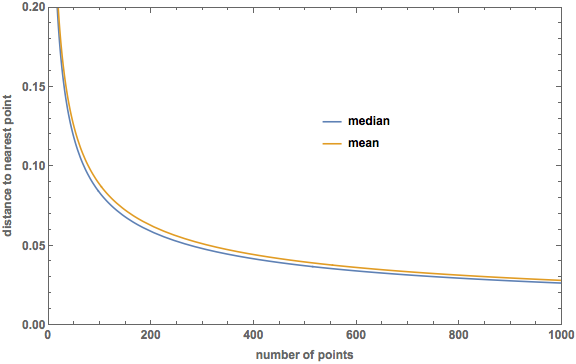
In 2 dimensions, the mean is not always greater than the median. Here is a plot of the difference:
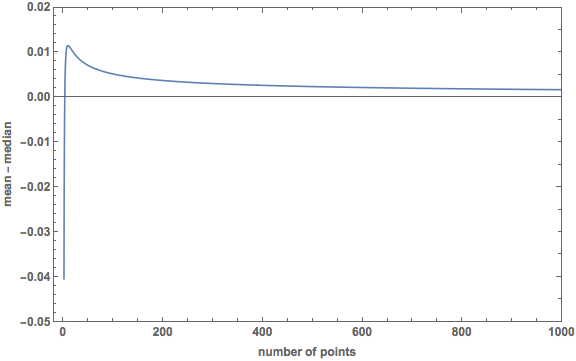
The mean starts out smaller than the median, and they are equal at \(N = 2.6237\). The peak in the plot (when the mean is most greater than the median), occurs at \(N = 0.9807\) and the value of the difference here is \(0.0115\).
To generalize this to \(p\)-dimensions, the probability that \((N-1)\) points are at a distance \(> r\) is now \((1 - r^p)^{N-1}\) (look back at my post on the median distance for an explanation). The probability that one point is at \(r\) is \[\frac{ A_{p-1}(r) \text{d}r }{V_p(1)}, \] where \(A_p(r)\) is the surface area of the \(p\)-sphere of radius \(r\) (recall the the \(p\)-sphere is the boundary of the \((p+1)\)-ball, so the 1-sphere is what we ordinarily call a circle and has \(A_1 = 2 \pi r\)). Through some relations between area and volume (check the Wikipedia page if you are interested), it is possible to reduce this to the simple form \[\frac{ A_{p-1}(r) \text{d}r }{V_p(1)} = p r^{p-1} \text{d}r. \] Again we have to multiply by the combinatorical factor \(N\), and the expectation integral in \(p\)-dimensions becomes \[\text{E}(r) = \int_0^1 N p r^p (1-r^p)^{N-1} \text{d} r = \frac{N}{p} \frac{\Gamma(N)\Gamma(\frac{1}{p})}{\Gamma(1 + N + \frac{1}{p})}.\] The integral was done in Mathematica and verified using the Gradshteyn and Ryzhik reference above. Here is a plot of the mean distance to the nearest point for dimensions 2, 10, and 100. On this scale, the median lines are barely visually distinguishable from the mean lines, so I did not include them.
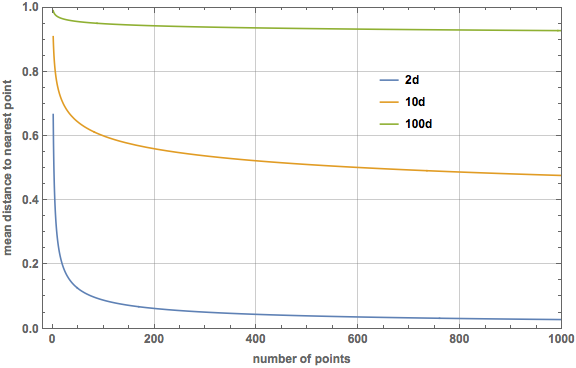
So the curse of dimensionality is evident using the mean instead of the median, just with a much more difficult (but fun) calculation!