In my last post, I calculated the mean distance to the nearest point to the origin among $N$ points taken from a uniform distribution on $[-1, 1]$. This turned out to be $r = 1/(N+1)$, which is close to but greater than the median distance $m = 1 - (1/2)^{1/N}$.
In this post, I want to generalize the calculation of the mean to a $p$-dimensional uniform distribution over the unit ball. To start things off, let’s look at the specific case $p = 2$ (a circle). It is often easier to see a generalization after performing the calculation in a few easy (low) dimensional cases.
Following the same form of reasoning as in the previous post, we want to calculate $$ \Pr(\text{closest point is at } r) = \Pr(\text{all other points are } > r) \times \Pr(\text{one point is at } r). $$ The probability that all other points $(N - 1)$ are at distances greater than $r$ is $(1-r^2)^{N-1}$. The probability that one point is at a distance $r$ is the ratio of the infinitesimal area at $r$ to the entire area of the unit circle: $$ \frac{2 \pi r, \mathrm{d}r}{\pi} = 2 r, \mathrm{d}r. $$ We also have to mutiply by an overall factor of $N$ to account for the $N$ different ways of labelling the closest point. Putting everything together: $$ \Pr(\text{closest point is at } r) = 2 r N (1- r^2)^{N-1} \mathrm{d} r, $$ and to get the mean value of $r$ we multiply by $r$ and integrate: $$ \operatorname{E}(r) = \int_0^1 2 r^2 N (1-r^2)^{N-1} \mathrm{d}r = N \sqrt{\frac{\pi}{4}} \frac{\Gamma(N)}{\Gamma \left(N + \frac{3}{2}\right)}. $$ I used Mathematica to carry out the integral and verified the answer with Gradshteyn and Ryzhik, 3.251, number 1 (page 324 in the 7th edition). In Gradshteyn and Ryzhik, the integral is given in terms of the beta function (Euler integral of the first kind): $$ B(x, y) = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}. $$ I don’t see a nice simplified form, and Mathematica doesn’t seem to be able to find one.
Here is a plot made in Mathematica comparing the median distance to the nearest point ($m = (1 - (1/2)^{1/N})^{1/2}$) to the mean:
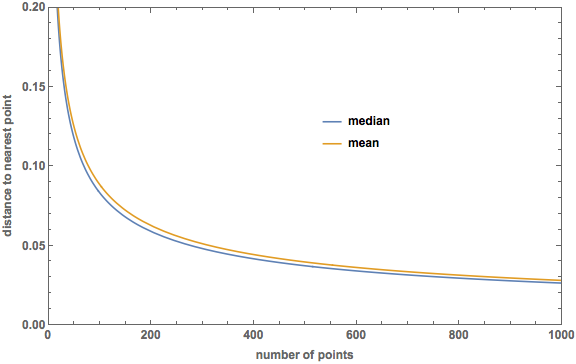
In 2 dimensions, the mean is not always greater than the median. Here is a plot of the difference:
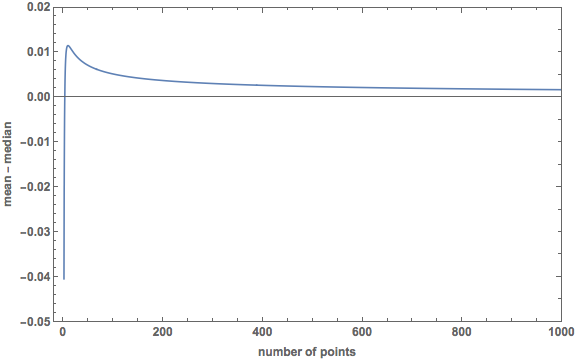
The mean starts out smaller than the median, and they are equal at $N = 2.6237$. The peak in the plot (when the mean is most greater than the median) occurs at $N = 0.9807$ and the value of the difference here is $0.0115$.
To generalize this to $p$ dimensions, the probability that $(N-1)$ points are at a distance $> r$ is now $(1 - r^p)^{N-1}$ (look back at my post on the median distance for an explanation). The probability that one point is at $r$ is $$ \frac{A_{p-1}(r) \mathrm{d}r}{V_p(1)}, $$ where $A_p(r)$ is the surface area of the $p$-sphere of radius $r$ (recall that the $p$-sphere is the boundary of the $(p+1)$-ball, so the 1-sphere is what we ordinarily call a circle and has $A_1 = 2 \pi r$). Through some relations between area and volume (check the Wikipedia page if you are interested), it is possible to reduce this to the simple form $$ \frac{A_{p-1}(r) \mathrm{d}r}{V_p(1)} = p r^{p-1} \mathrm{d}r. $$ Again we have to multiply by the combinatorial factor $N$, and the expectation integral in $p$ dimensions becomes $$ \operatorname{E}(r) = \int_0^1 N p, r^p (1-r^p)^{N-1} \mathrm{d} r = \frac{N}{p} \frac{\Gamma(N)\Gamma \left(\frac{1}{p}\right)}{\Gamma \left(1 + N + \frac{1}{p}\right)}. $$ The integral was done in Mathematica and verified using the Gradshteyn and Ryzhik reference above. Here is a plot of the mean distance to the nearest point for dimensions 2, 10, and 100. On this scale, the median lines are barely visually distinguishable from the mean lines, so I did not include them.
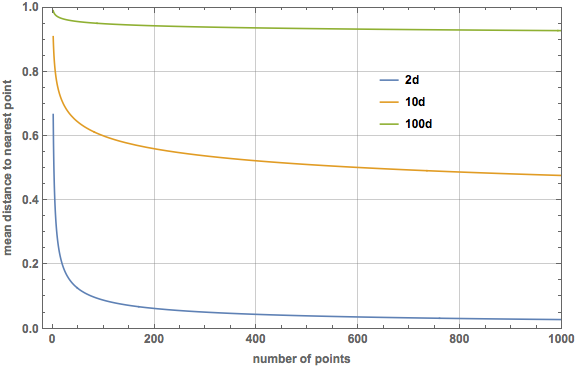
So the curse of dimensionality is evident using the mean instead of the median, just with a much more difficult (but fun) calculation!