The problem
Consider a function \(f: [0, 1] \to \mathbb{R}\) that is continuous with \(f(0) = f(1)\). It is possible to prove that for each \(n \in \mathbb{N}\), there exist \(x_n, y_n \in [0, 1]\) such that \(|x_n - y_n| = 1/n\) and \(f(x_n) = f(y_n)\). This means the set of points at which the function is not one-to-one is at least countably infinite. Providing the proof is part of Exercise 4.5.6 in Abbott’s Understanding Analysis (2nd edition).
I’m not going to discuss the proof here, but I am interested in the final part of the exercise, which asks for a specific counterexample. Quoting Abbott:
If \(h \in (0, 1)\) is not of the form \(1/n\), there does not necessarily exist \(|x - y| = h\) satisfying \(f(x) = f(y)\). Provide an example that illustrates this using \(h = 2/5\).
I found this perhaps harder than it should have been. Restating the problem slightly, we are looking for a function \(f\) such that \(f(x + 2/5) - f(x) \neq 0\), for all \(x \in [0, 3/5]\) (since \(3/5 = 1 - 2/5\)), while satisfying the requirement that \(f(0) = f(1)\).
A specific counterexample
After some trial and error, I hit on the idea of using a function that does have a period of \(2/5\), and then modifying it somehow. Starting with \(\sin\): \[ \sin\left(\frac{5}{2}2\pi x\right) \] has a period of \(2/5\), since \[ \sin\left[\frac{5}{2}2\pi \left(x + \frac{2}{5}\right)\right] = \sin\left(\frac{5}{2} 2\pi x + 2 \pi\right) = \sin\left(\frac{5}{2}2 \pi x\right). \]
Now for the desired function \(f\), try a function of the form \[ f(x) = \sin\left(\frac{5}{2}2\pi x\right) + a x .\] Requiring that \(f(0) = f(1)\) means that \[a = - \sin\left(\frac{5}{2}2\pi\right) = 0,\] so this functional form won’t work.
Instead of \(\sin\), lets try \(\cos\): \[ \cos\left(\frac{5}{2}2\pi x\right) \] has a period of \(2/5\), and trying the same kind of functional form: \[f(x) = \cos\left(\frac{5}{2}2\pi x\right) + a x \], we see that \(f(0) = 1\) and \(f(1) = -1 + a\), so \(a = 2\) works. Calculating the difference \[ f(x + \frac{2}{5}) - f(x) = 2 \left(x + \frac{2}{5}\right) - 2x = \frac{4}{5}, \] so this is the desired counterexample! Here is a plot, along with a horizontal red line of length \(2/5\) shown at one point along the function:
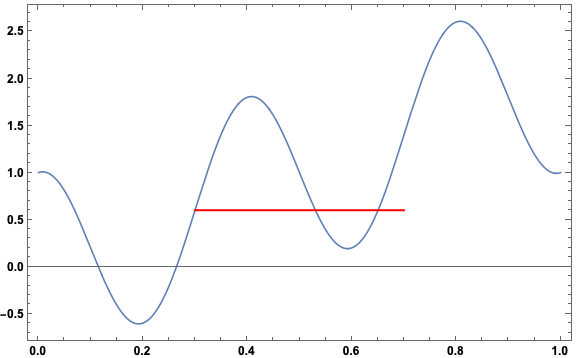
Imagine sliding the red line around on the function (keeping it horizontal). The two ends of the line never simultaneously interesect the function! In fact, a little experimentation shows that the line is not optimal, in the sense that it could be a bit shorter or a bit longer and still not intersect the function at both ends. So our counterexample \(f(x)\) is a counterexample for values of \(h\) close to \(2/5\) as well as for \(h = 2/5\).
Generalizing
The fact that the above function \(f(x)\) is a counterexample for values of \(h\) close to \(2/5\) shows that there is nothing special about \(2/5\). Specifically there is nothing special about the fact that it is rational. So let’s try to find a function for arbitrary values of \(h \in (0, 1)\).
First, note that we can take care of many values of \(h\) at once by using the simple function \[f(x) = \sin(2\pi x). \] If \(h > 1/2\) and \(x < 1/2\) then \(f(x + h) = -f(x)\), so \(f(x + h) - f(x) = -2 f(x) < 0\). We don’t have to consider larger values of \(x\) since the property \(f(x + h) \neq f(x)\) only needs to hold for \(x \in [0, 1 - h]\). This shows that there does not necessarily exist \(h \in (1/2, 1)\).
For arbitrary \(h \in (0, 1/2)\), let’s try a function of the same form as the specific counterexample above: \[ f(x) = \cos\left(\frac{2\pi x}{h}\right) + a x.\] Then \(f(0) = 1\) and \(f(1) = \cos\left(\frac{1}{h}2\pi\right) + a\), so the desired form is \[ \boxed{ f(x) = \cos\left(\frac{2\pi x}{h}\right) + \left(1 - \cos\left(\frac{2\pi}{h}\right)\right)x .} \]
Calculating the difference: \[ f(x + h) - f(x) = h \left(1 - \cos\left(\frac{2\pi}{h}\right)\right) = 2 h \sin^2\left(\frac{\pi}{h}\right),\] using a half-angle formula.
The difference is greater than zero for all values of \(h\) except for \(h\) such that \(\sin(\pi/h) = 0\), which are exactly the values \(1/n, n \in \mathbb{N}\) for which there is always at least one place where the function is not one-to-one!
Here is a plot of the difference \(f(x + h) - f(x) = 2 h \sin^2\left(\frac{\pi}{h}\right)\) as a function of \(h\):
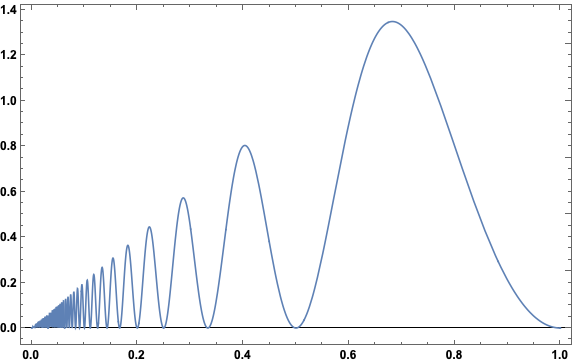
It only intersects zero at the countably infinite set of points \(1/n, n \in \mathbb{N}\).
Summary
Any continuous function \(f:[0, 1] \to \mathbb{R}\) satisfying \(f(0) = f(1)\) must fail to be one-to-one for at least one pair of points in \([0, 1]\) separated by \(h = 1/n\), and this is true for all \(n \in \mathbb{N}\). Furthermore, by the counterexample given above, there are no other “separations” \(h \in (0, 1)\) for which non-injectivity is guaranteed!
Is there another general functional form that provides a counterexample for arbitrary values of \(h \neq 1/n\)? Let me know if you find one!